Relation entre la rotation et le rayon de courbure :
Soient deux sections infiniment proches dont la variation d’abscisse vaut dx.
La variation de la rotation de la section en x à la section en x + dx vaut dω.
On démontre que:
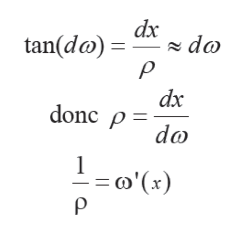
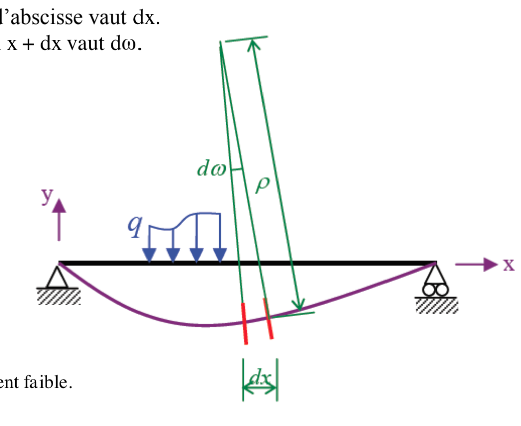
la rotation dω peut être assimilée à sa tangente car elle est infiniment faible.
Relation entre la flèche et le moment :
En combinant les différentes relations on obtient:
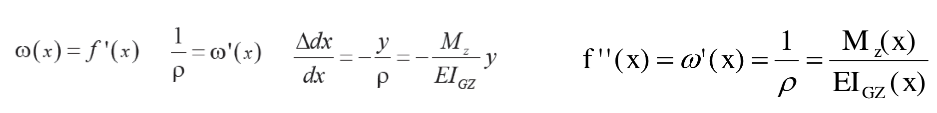
En résumé:
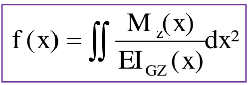
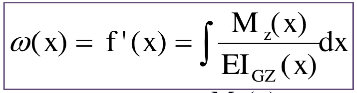
En intégrant deux fois l’expression des constantes d’intégration apparaissent.
Afin de déterminer leurs valeurs, il est nécessaire de connaître la flèche ou la rotation en certains points
particuliers.
Nous savons que les appuis bloquent des mouvements :
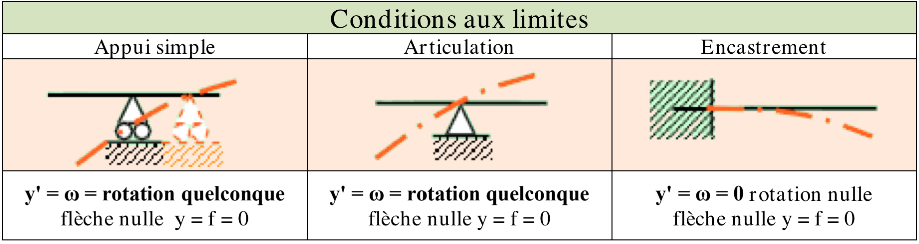
Au sommaire
- RAPPELS RdM FONDAMENTAUX
- Poutres hyperstatiques (Poutre bi-encastrée avec force ponctuelle):
- Flèches associées (Poutre bi-encastrée avec force ponctuelle)
- Méthode formule des 3 moments(Poutre bi-encastrée avec force ponctuelle)
- Poutres hyperstatiques (Poutre bi-encastrée avec chargement uniforme)
- Flèches associées (Poutre bi-encastrée avec chargement uniforme)
- Méthode formule des 3 moments (Poutre bi-encastrée avec chargement uniforme)
- Poutres hyperstatiques (Poutre Encastrée + appui simple avec chargement uniforme)
- Méthode formule des 3 moments. (Poutre Encastrée + appui simple avec chargement uniforme)
- Console avec charge triangulaire:
- Calcul des déformées charge triangulaire
- Méthode des intégrales de Mohr (Charge Triangulaire)
