Ce cours correspond au module MEC441 de l’École Polytechnique. Il a pour objectif de fournir les outils de base pour appréhender le calcul de structures sous des hypothèses simplificatrices qui peuvent être fortes. Il n’a pas vocation à couvrir le calcul de structures au sens le plus large.
Table des matières
Introduction
Le génie civil est une discipline très vaste. Elle regroupe les constructions civiles, du tunnel ferroviaire à la centrale nucléaire, en passant par le pont, le barrage et le bâtiment. Les principes structurels de ces constructions sont très variés, comme l’arc, la voûte, le fonctionnement en poteau-poutre, la toile tendue, le pont suspendu, le pont haubané, le treillis, etc. Ces différents types de structures s’expriment dans différents matériaux comme l’acier, le béton, le bois, mais aussi le verre, les matériaux composites et d’autres. Les métiers du génie civil sont également très nombreux, selon le domaine (géotechnique, thermique, structure, etc.) ou l’étape du projet de construction (bureau d’étude, méthodes, suivi de chantier, planning, etc.).
Dans ce polycopié, nous ne nous intéresserons qu’aux structures, c’est-à-dire aux éléments qui permettent le transfert des charges jusqu’au support, le sol. En pratique, leur calcul se fait généralement à l’aide de simulations numériques et les résultats doivent vérifier les codes de constructions réglementaires. Il est néanmoins souvent possible d’appréhender le comportement d’une structure à la main. Cela permet d’en comprendre le fonctionnement rapidement et d’éviter l’usage de méthodes numériques qui sont lourdes et dont les incertitudes, souvent oubliées, peuvent être grandes. Nous présenterons ici les méthodes classiques de calcul de structures isostatiques (cf. Chapitre 3) composées d’éléments dont une longueur est grande devant les deux autres (poutres), sous certaines hypothèses (cf. Chapitre 2) qui sont suffisamment peu restrictives pour être bien souvent valides. La figure 6.2 page 35 synthétise la structure du polycopié.
Le formalisme présenté ici a pour but de faire le lien avec la mécanique des milieux continus et de satisfaire le lecteur curieux. Néanmoins, la finalité de ce document est de fournir des outils concrets et applicables, aussi le lecteur plus pressé pourra ne s’arrêter que sur les encadrés.
Définitions
1.1 Notion de poutre
Définition 1.1.1 — Poutre. On appelle poutre un solide engendré par une surface plane (Σ) qui peut être variable et dont le centre de gravité G décrit un segment [AB], le plan de (Σ) restant perpendiculaire à cette courbe. Il faut également que la longueur AB soit grande devant les dimensions des sections transverses.
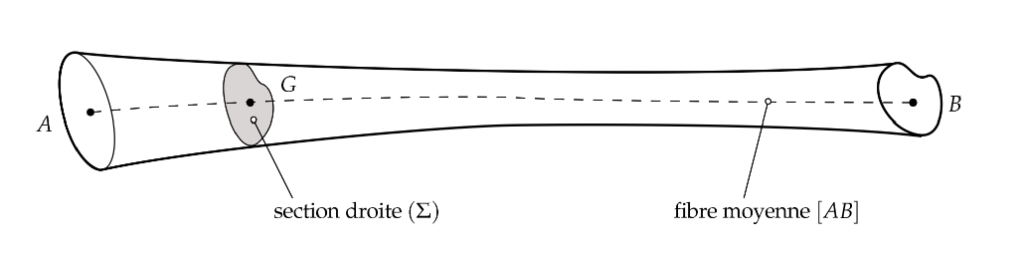
Une poutre est donc un volume dont une dimension est grande devant les deux autres.
De manière analogue, une coque est un volume dont deux dimensions sont grandes devant la troisième.
Définition 1.1.2 — Section droite, fibre moyenne. (Σ) est appelée section droite, (AB) est la fibre moyenne de la poutre (ou ligne moyenne ou encore lieu des centres d’inertie des sections droites de la poutre).
Définition 1.1.3 — Fibre neutre. La ligne d’allongement nul en flexion pure est appelée fibre neutre (ou ligne neutre).
Sous l’hypothèse des petites déformations (voir Chapitre 2), la fibre neutre et la fibre moyenne sont confondues.
Géométrie des poutres : cas usuels
Si la fibre moyenne (AB) de la poutre est :
- contenue dans un plan, on parle de poutre plane (ou poutre à plan moyen) ;
- une droite, on parle de poutre droite ;
- courbe, on parle de poutre gauche.
La section droite (Σ) peut être :
- constante le long de (AB), on parle alors de poutre à section constante ;
- variable, on parle alors de poutre à section variable ; en pratique, l’intérêt d’une telle poutre est de s’adapter aux efforts qu’elle supporte et donc d’optimiser l’emplacement de la matière.
Dans la mesure où la complexité apportée par la tridimensionnalité est formelle plus que substantielle, les poutres étudiées en exemples ici sont planes. En outre, elles sont à sections constantes et généralement droites.
1.3 Repère central principal d’inertie
Définition 1.3.1 — Centre d’inertie. Le centre d’inertie G d’un solide S de masse volumique ρ(M) en M ∈ S est le barycentre des masses, c’est-à-dire que si O est le centre du repère :
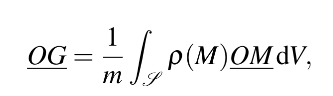
Le centre de gravité étant le barycentre des poids, le confondre avec le centre d’inertie revient à négliger les variations de la pesanteur. L’erreur commise est très faible en pratique, même pour les plus grandes structures du génie civil.
Définition 1.3.2 — Opérateur d’inertie. On appelle opérateur d’inertie au point P du solide S l’application qui à tout u ∈ R 3 associe le vecteur .
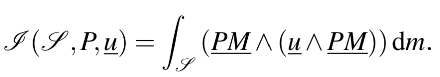
L’opérateur d’inertie définit la répartition de la masse d’un solide autour d’un de ses points P. Il s’agit d’un opérateur linéaire en u et peut donc être représenté par une matrice dans une base donnée. Par exemple dans une base (e1, e2, e3) de R3, O le centre du repère considéré et
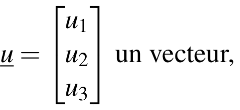
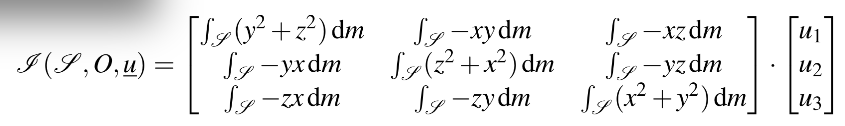
Soit G le centre d’inertie d’une section droite (Π) et I (S ,G,·) l’opérateur d’inertie de (Π) en G. I (S ,G,·) est symétrique défini positif. Ses vecteurs propres (perpendiculaires et normés) dans le plan de la section Π sont notés Iy et Iz.
Définition 1.3.3 — Repère central principal d’inertie. En tout point G de la fibre moyenne, le repère central principal d’inertie est le repère noté R = (Gxyz), centré en G et formé par les vecteurs propres principaux de l’opérateur d’inertie du solide en G.

1 Commentaire
c est intéressant est ce que je peux avoir des exercice et corrigés de structure