Table of Contents
Marche à suivre
- Généralités
- Calcul du plancher (dalle)
- Calcul des poutres
- Calcul des poteaux
- Calcul de la fondation
- Calcul de l’escalier
Généralités
Les éléments de calcul figurant dans cette note et les règles de calcul du béton armé sont conformes aux règles techniques de conception et de calcul des ouvrages et constructions en béton armé, suivant la méthode des états limites (BS 8110).
1-Définitions et principe des justifications
1.1. Domaine d’application des règles
Les règles de calcul B.S sont applicables à tous les ouvrages et constructions en béton armé dont le béton est constitué de granulats naturels normaux avec un dosage en ciment au moins égal à 300kg/m3 de béton mis en œuvre.
On distingue les constructions courantes, les constructions industrielles et les constructions spéciales.
Dans les constructions courantes, les charges d’exploitation sont dites modérées et sont au plus égales à deux fois celles des charges permanentes ou à 5000N/m2.
Les constructions suivantes entrent normalement dans cette catégorie :
- les bâtiments à usage d’habitation ou d’hébergement
- les bâtiments à usage de bureau
- les constructions scolaires
- les constructions hospitalières
Dans les constructions industrielles, les charges d’exploitation sont relativement élevées et sont supérieures à deux fois celles des charges permanentes ou à 5 000N/m2.
Les constructions suivantes entrent normalement dans cette catégorie :
- les bâtiments industriels (usines, ateliers, etc.)
- les entrepôts.
Dans les constructions spéciales, certaines parties de la structure peuvent être assimilées à des éléments de constructions courantes, d’autres à des éléments de
constructions industrielles.
Les constructions suivantes restent en dehors du domaine d’application des règles de calcul:
- les constructions en béton non armé ;
- les constructions en béton constitué de granulats légers ;
- les structures mixtes acier-béton ;
les éléments soumis à des températures s’écartant de celles qui résultent des seules influences climatiques (caissons de pile atomique).
1.2. Principe des justifications
Les calculs justificatifs sont conduits suivant la théorie des états limites. Un état limite est celui pour lequel une condition requise d’une construction est strictement satisfaite et cesserait de l’être en cas de modification défavorable d’une action.
On distingue les états limites ultimes (E.L.U.) et les états limites de service (E.L.S.)
Les états limites ultimes correspondent à la limite :
- soit de l’équilibre statique ;
- soit de la résistance de l’un des matériaux acier ou béton (E.L.U.R.);
- soit de la stabilité de forme (E.L.U.S.F.)
Les états limites de service sont définis compte tenu des conditions d’exploitation ou de durabilité. On distingue :
- les états limites de service vis-à-vis de la durabilité de la structure :
- état limite de compression du béton ;
- état limite d’ouverture des fissures.
- les états limites de service vis-à-vis des déformations.
La méthode de calcul aux états limites est une méthode de calcul semi probabiliste avec coefficients de sécurité partiels. On applique des coefficients de sécurité aux valeurs caractéristiques de résistance des matériaux ainsi qu’aux actions qui s’exercent sur la structure.
Si l’on se limitait à des calculs à la rupture, en affectant des coefficients de sécurité aux actions, on ne pourrait se rendre compte du comportement de l’ouvrage en service vis-à-vis des déformations, de la contrainte maximale de compression du béton ou de l’ouverture des fissures. Il faut donc, en plus du calcul à la rupture, limiter les contraintes dans les éléments de la structure aux valeurs fixées par le règlement.
Le mixage entre ces deux approches conduit à la méthode de calcul aux états limites.
2-Actions et sollicitations
2.1. Actions
Les trois types d’actions appliquées à une structure sont les actions permanentes, les actions variables et les actions accidentelles
Les actions permanentes, notées G, représentent des actions dont l’intensité est
constante ou très peu variables dans le temps. Elles comprennent notamment :
- le poids propre de la structure ;
- le poids propre des éléments fixes ;
- les effets dus à des terres ou des liquides dont les niveaux varient peu.
Les actions variables, notées Q, représentent des actions dont l’intensité varie fréquemment et de façon très importante dans le temps.
Les actions accidentelles proviennent des phénomènes rares et ne sont à considérer que si les documents d’ordre public ou le marché les prévoient. Elles comprennent notamment :
- les chocs de véhicule ou de bateaux sur les appuis de ponts ;
- les séismes ;
- les explosions, les chutes de rochers.
2.2. Calcul des sollicitations
Les sollicitations sont les efforts (effort normal et effort tranchant) et les moments (moment fléchissant et moment de torsion) calculés à partir des actions par des méthodes appropriées.
2.2.1. Notations
On considère les actions suivantes :
- Gmax : l’ensemble des actions permanentes défavorables
- Gmin : l’ensemble des actions permanentes favorables
- Q1 : action variable de base
- Qi : autres actions variables d’accompagnement (i>1)
Dans une action donnée, Gmax et Gmin désignent des actions d’origine et de nature différentes, ce qui exclut de partager une même action permanente entre ces deux parties. En particulier, le poids propre d’une poutre continue est introduit avec le même coefficient sur toute la longueur.
2.2.2. Hypothèses et principe de calcul des sollicitations
Une construction peut être soumise à un grand nombre de combinaisons d’actions dont on retiendra les plus défavorables.
Il faut donc procéder en deux étapes :
- établir les différentes combinaisons d’actions
- rechercher la combinaison d’actions la plus défavorable vis-à-vis de l’état limite étudié.
2.2.3. Sollicitations de calcul vis-à-vis des états limites ultimes de résistance
Les sollicitations à considérer résultent des combinaisons d’actions suivantes :
Combinaisons fondamentales 1,35Gmax+Gmin+γQ1Q1+∑1,3ψ2iQi
où γQ1 vaut 1,5 dans le cas général et 1,35 dans les cas suivants :
- la température
- les charges d’exploitation étroitement bornées ou de caractère particulier (convois militaires, convois exceptionnels)
- les bâtiments agricoles à faible densité d’occupation humaine.
Combinaisons d’actions accidentelles 1,35Gmax+Gmin+FA+ψ11Qi+∑ψ2iQi
avec FA : valeur nominale de l’action accidentelle
ψ11.Qi : valeur fréquente d’une action variable
ψ2i.Qi : valeur quasi permanente d’une autre action variable
2.2.4. Sollicitations de calcul vis-à-vis des états limites de service
Les sollicitations de calcul vis-à-vis des états limites de service résultent des
combinaisons d’actions suivantes :
Combinaisons rares Gmax+Gmin+Q1+∑ψ0iQi
3-Les matériaux acier et béton
Pour pouvoir dimensionner des éléments en béton armé, il est indispensable de
connaître le comportement des matériaux acier et béton et d’être capable de les
modéliser.
3.1. Modélisation du béton
3.1.1. Résistance caractéristique
Résistance caractéristique à la compression
Pour l’établissement des projets, un béton est défini par une valeur de résistance à la compression à l’âge de 28 jours, dite valeur caractéristique requise et notée fc28.
Résistance caractéristique à la traction
La résistance caractéristique à la traction du béton à j jours est notée ftj et est conventionnellement définie par la relation suivante :
ftj= 0,6+0,06 x fcj
3.1.2. Déformations longitudinales du béton
L’expression ci-dessous permet de déterminer la valeur du module de déformation longitudinale instantanée du béton soumis à des contraintes d’une durée d’application inférieure à 24 heures :
Eij=11 000 x [fcj] 1/3
Sous des contraintes de longue durée d’application, on admet que le module de
déformation longitudinale différée est égal à l’expression suivante :
Evj=3 700 x [fcj] 1/3
3.1.3. Diagramme déformations-contraintes
Le diagramme déformations-contraintes du béton pouvant être utilisé lors d’une justification à l’état limite ultime de résistance est le diagramme dit «parabole-
rectangle».
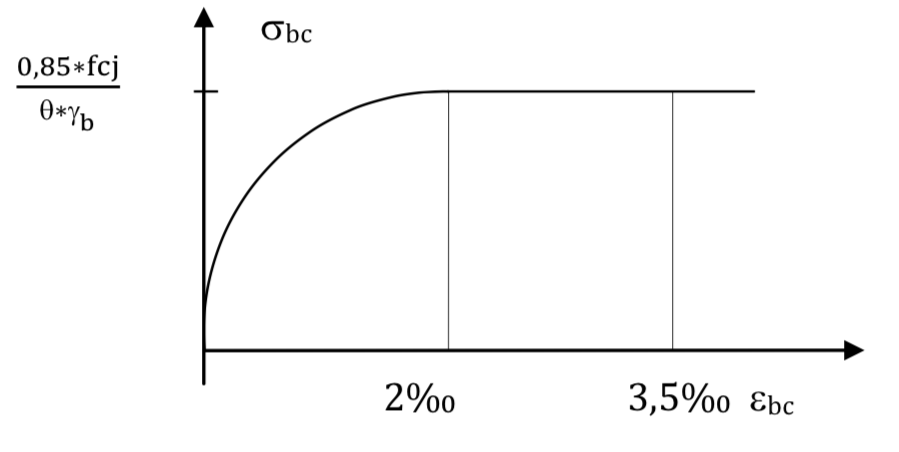
Le coefficient b est égal à 1,5 pour les combinaisons fondamentales et à 1,15 pour les combinaisons accidentelles.
Le coefficient est fixé à 1 lorsque la durée probable d’application de la combinaison d’actions considérée est supérieure à 24 heures, à 0,9 lorsque cette durée est comprise entre une heure et 24 heures, et à 0,85 lorsqu’elle est inférieure à une heure.
3.2. Modélisation de l’acier
En génie civil, on rencontre plusieurs types d’armatures : les armatures à haute adhérence et les treillis soudés.
3.2.1. Caractéristiques mécaniques
Le tableau ci-dessous donne les caractéristiques mécaniques des différents types d’armatures.
Désignation | Symbole | Nuance FeE | Limite d’élas– ticité (MPa) | Résistance à la traction (MPa) | Allongement de rupture (%) |
Barres à haute adhérence | HA | 400 | 400 | 480 | 14 |
HA | 500 | 500 | 550 | 12 | |
Treillis soudés | TS | 500 | 500 | 550 |
3.2.2. Module d’élasticité longitudinale
Le module d’élasticité longitudinale de l’acier est égal à la valeur suivante :
Es= 2 x 105MPa
3.2.3. Diagramme déformation-contraintes
Lors d’une justification à l’état limite ultime, le diagramme déformations-contraintes à considérer est conventionnellement défini ci-dessous :
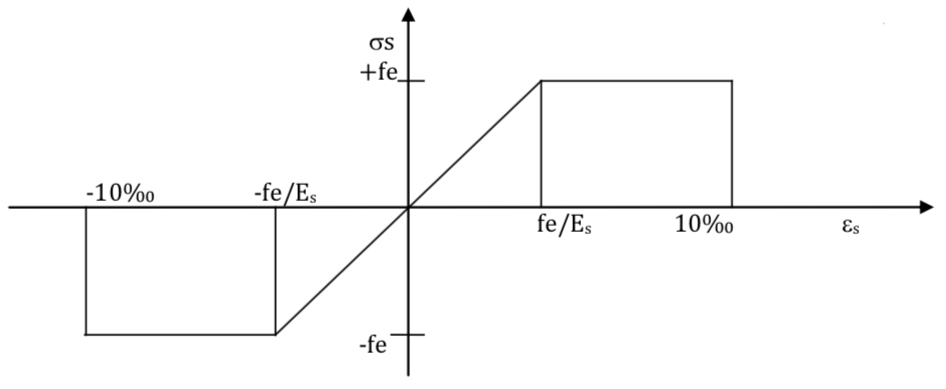
3.2.4. Caractéristiques géométriques
Barres à haute adhérence
Ø (mm) | 6 | 8 | 10 | 12 | 14 | 16 | 20 | 25 | 32 | 40 |
Section (mm2) | 28,27 | 50,27 | 78,54 | 113,1 | 153,94 | 201,06 | 314,16 | 490,87 | 804,25 | 1256,64 |
Poids (kg/m) | 0,222 | 0,395 | 0,617 | 0,888 | 1,208 | 1,578 | 2,466 | 3,854 | 6,313 | 9,864 |
4-Association acier-béton
4.1. Adhérence des aciers en barres
4.1.1. Contrainte d’adhérence
La liaison entre une armature et le béton est mesurée par la contrainte d’adhérence τs définie par la formule suivante :
τs= 1.dF / u.dx
où dF/dx est la variation par unité de longueur de l’effort axial exercé sur l’armature et u le périmètre utile de l’armature.
4.1.2. Ancrage des aciers en barres
On suppose que la contrainte d’adhérence est constante sur la longueur de l’ancrage et est égale à sa valeur ultime :
τsu=0,6 x ψ2s x ftj
où ψs est le coefficient de scellement qui caractérise l’efficacité d’une barre du point de vue de l’adhérence. Il est égal à l’unité pour les barres lisses et à 1,5 pour les armatures à haute adhérence.
Ancrage rectiligne
On considère une armature, de diamètre D, scellée dans un massif de béton et soumise à un effort de traction Fmax. On note ls la longueur de scellement droit de la barre.
L’équation d’équilibre de la barre permet de déterminer l’expression de la longueur de scellement droit :
τsu x π x D x ls=fe x π x D2/4
.
D’où l’on tire ls= fe x D / 2.4 x ψ2s x ftj
En général, ls=50 est une valeur forfaitaire adoptée pour les aciers HA à défaut de
calculs plus précis.
Ancrages courbes
Il est nécessaire de réaliser un ancrage courbe lorsqu’il n’y a pas suffisamment de place pour un ancrage rectiligne. La réalisation d’un ancrage courbe nécessite le façonnage de l’armature.
On définit, pour les armatures à haute adhérence, des crochets aux dimensions fixées appelés crochets normaux, pour lesquels on peut se dispenser d’effectuer un calcul d’ancrage courbe. Le respect des prescriptions concernant le crochet normal dispense également de vérifier la condition de non-écrasement du béton.
4.1.3. Longueur de recouvrement des armatures tendues
Dans certains cas, pour assurer la continuité de la transmission des efforts, il faut
réaliser une jonction par recouvrement entre deux barres identiques sur une certaine longueur appelée «longueur de recouvrement» et notée «L ».
Si les barres sont espacées d’une distance «c» inférieure à 5 fois leur diamètre, la longueur de recouvrement est égale à la longueur de scellement droit Ls.
En d’autres termes, si c 5 , L =L
Si les barres sont espacées de plus de 5 fois leur diamètre, la transmission de l’effort d’une barre à l’autre se fait à travers des bielles de béton à 45° situées dans le plan des deux barres. La longueur de recouvrement est égale à la longueur de scellement droit plus la distance «c» entre les deux barres.
En d’autres termes, si c> 5 , L =L + c
4.2. Dispositions constructives diverses
4.2.1. Protection des armatures
Le bon fonctionnement de l’association acier-béton n’est effectif que si les armatures sont correctement enrobées de béton. L’enrobage est défini comme étant la distance de l’axe d’une armature à la paroi la plus voisine diminuée du rayon nominal de cette armature. Un enrobage correct assurera la bonne transmission des efforts du béton aux armatures, l’acier se substituant alors efficacement au béton tendu défaillant.
L’enrobage d’une cage d’armatures doit respecter des valeurs minimales qui sont
fonction du type d’ouvrage :
- e =5cm pour les ouvrages à la mer ou exposés aux embruns ou aux brouillards salins, ainsi que pour les ouvrages exposés à des atmosphères agressives.
- e =3cm pour des parois coffrées ou non qui sont soumises à des intempéries ou des condensations.
- e =1cm pour des parois situées dans des locaux couverts et clos et qui ne sont pas exposés aux condensations.
4.2.2. Possibilités de bétonnage correct.
L’enrobage de chaque armature est au moins égal à son diamètre si elle est isolée, ou à la largeur du paquet dont elle fait partie dans le cas contraire.
De même, la distance entre 2 armatures doit être au moins égale à leur diamètre si elles sont isolées, ou à la largeur des paquets dont elles font partie dans le cas contraire. En outre, cette distance doit être au moins égale à la dimension du plus gros granulat, cg, dans la direction verticale et à 1,5cg dans la direction horizontale.
4.2.3. Poussée au vide.
Lorsque des aciers non rectilignes sont en traction, il se développe des contraintes dans le béton avoisinant qui risquent de le faire éclater : c’est le phénomène de poussée au vide. L’armature ne doit pas être placée trop près de la paroi, au risque de la faire éclater; sinon une ligature est mise en place afin d’ancrer la barre dans le béton.
